第8课: 机器学习初步
from sklearn import datasets
from sklearn import cross_validation
from sklearn import linear_model
from sklearn import metrics
from sklearn import tree
from sklearn import neighbors
from sklearn import svm
from sklearn import ensemble
from sklearn import cluster
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
1. Built in datasets
boston = datasets.load_boston()
boston.keys()
['data', 'feature_names', 'DESCR', 'target']
print boston.DESCR
Boston House Prices dataset
Notes
------
Data Set Characteristics:
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive
:Median Value (attribute 14) is usually the target
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10,000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000's
:Missing Attribute Values: None
:Creator: Harrison, D. and Rubinfeld, D.L.
This is a copy of UCI ML housing dataset.
http://archive.ics.uci.edu/ml/datasets/Housing
This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980. N.B. Various transformations are used in the table on
pages 244-261 of the latter.
The Boston house-price data has been used in many machine learning papers that address regression
problems.
**References**
- Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
- Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
- many more! (see http://archive.ics.uci.edu/ml/datasets/Housing)
boston.data
array([[ 6.32000000e-03, 1.80000000e+01, 2.31000000e+00, ...,
1.53000000e+01, 3.96900000e+02, 4.98000000e+00],
[ 2.73100000e-02, 0.00000000e+00, 7.07000000e+00, ...,
1.78000000e+01, 3.96900000e+02, 9.14000000e+00],
[ 2.72900000e-02, 0.00000000e+00, 7.07000000e+00, ...,
1.78000000e+01, 3.92830000e+02, 4.03000000e+00],
...,
[ 6.07600000e-02, 0.00000000e+00, 1.19300000e+01, ...,
2.10000000e+01, 3.96900000e+02, 5.64000000e+00],
[ 1.09590000e-01, 0.00000000e+00, 1.19300000e+01, ...,
2.10000000e+01, 3.93450000e+02, 6.48000000e+00],
[ 4.74100000e-02, 0.00000000e+00, 1.19300000e+01, ...,
2.10000000e+01, 3.96900000e+02, 7.88000000e+00]])
boston.target
array([ 24. , 21.6, 34.7, 33.4, 36.2, 28.7, 22.9, 27.1, 16.5,
18.9, 15. , 18.9, 21.7, 20.4, 18.2, 19.9, 23.1, 17.5,
20.2, 18.2, 13.6, 19.6, 15.2, 14.5, 15.6, 13.9, 16.6,
14.8, 18.4, 21. , 12.7, 14.5, 13.2, 13.1, 13.5, 18.9,
20. , 21. , 24.7, 30.8, 34.9, 26.6, 25.3, 24.7, 21.2,
19.3, 20. , 16.6, 14.4, 19.4, 19.7, 20.5, 25. , 23.4,
18.9, 35.4, 24.7, 31.6, 23.3, 19.6, 18.7, 16. , 22.2,
25. , 33. , 23.5, 19.4, 22. , 17.4, 20.9, 24.2, 21.7,
22.8, 23.4, 24.1, 21.4, 20. , 20.8, 21.2, 20.3, 28. ,
23.9, 24.8, 22.9, 23.9, 26.6, 22.5, 22.2, 23.6, 28.7,
22.6, 22. , 22.9, 25. , 20.6, 28.4, 21.4, 38.7, 43.8,
33.2, 27.5, 26.5, 18.6, 19.3, 20.1, 19.5, 19.5, 20.4,
19.8, 19.4, 21.7, 22.8, 18.8, 18.7, 18.5, 18.3, 21.2,
19.2, 20.4, 19.3, 22. , 20.3, 20.5, 17.3, 18.8, 21.4,
15.7, 16.2, 18. , 14.3, 19.2, 19.6, 23. , 18.4, 15.6,
18.1, 17.4, 17.1, 13.3, 17.8, 14. , 14.4, 13.4, 15.6,
11.8, 13.8, 15.6, 14.6, 17.8, 15.4, 21.5, 19.6, 15.3,
19.4, 17. , 15.6, 13.1, 41.3, 24.3, 23.3, 27. , 50. ,
50. , 50. , 22.7, 25. , 50. , 23.8, 23.8, 22.3, 17.4,
19.1, 23.1, 23.6, 22.6, 29.4, 23.2, 24.6, 29.9, 37.2,
39.8, 36.2, 37.9, 32.5, 26.4, 29.6, 50. , 32. , 29.8,
34.9, 37. , 30.5, 36.4, 31.1, 29.1, 50. , 33.3, 30.3,
34.6, 34.9, 32.9, 24.1, 42.3, 48.5, 50. , 22.6, 24.4,
22.5, 24.4, 20. , 21.7, 19.3, 22.4, 28.1, 23.7, 25. ,
23.3, 28.7, 21.5, 23. , 26.7, 21.7, 27.5, 30.1, 44.8,
50. , 37.6, 31.6, 46.7, 31.5, 24.3, 31.7, 41.7, 48.3,
29. , 24. , 25.1, 31.5, 23.7, 23.3, 22. , 20.1, 22.2,
23.7, 17.6, 18.5, 24.3, 20.5, 24.5, 26.2, 24.4, 24.8,
29.6, 42.8, 21.9, 20.9, 44. , 50. , 36. , 30.1, 33.8,
43.1, 48.8, 31. , 36.5, 22.8, 30.7, 50. , 43.5, 20.7,
21.1, 25.2, 24.4, 35.2, 32.4, 32. , 33.2, 33.1, 29.1,
35.1, 45.4, 35.4, 46. , 50. , 32.2, 22. , 20.1, 23.2,
22.3, 24.8, 28.5, 37.3, 27.9, 23.9, 21.7, 28.6, 27.1,
20.3, 22.5, 29. , 24.8, 22. , 26.4, 33.1, 36.1, 28.4,
33.4, 28.2, 22.8, 20.3, 16.1, 22.1, 19.4, 21.6, 23.8,
16.2, 17.8, 19.8, 23.1, 21. , 23.8, 23.1, 20.4, 18.5,
25. , 24.6, 23. , 22.2, 19.3, 22.6, 19.8, 17.1, 19.4,
22.2, 20.7, 21.1, 19.5, 18.5, 20.6, 19. , 18.7, 32.7,
16.5, 23.9, 31.2, 17.5, 17.2, 23.1, 24.5, 26.6, 22.9,
24.1, 18.6, 30.1, 18.2, 20.6, 17.8, 21.7, 22.7, 22.6,
25. , 19.9, 20.8, 16.8, 21.9, 27.5, 21.9, 23.1, 50. ,
50. , 50. , 50. , 50. , 13.8, 13.8, 15. , 13.9, 13.3,
13.1, 10.2, 10.4, 10.9, 11.3, 12.3, 8.8, 7.2, 10.5,
7.4, 10.2, 11.5, 15.1, 23.2, 9.7, 13.8, 12.7, 13.1,
12.5, 8.5, 5. , 6.3, 5.6, 7.2, 12.1, 8.3, 8.5,
5. , 11.9, 27.9, 17.2, 27.5, 15. , 17.2, 17.9, 16.3,
7. , 7.2, 7.5, 10.4, 8.8, 8.4, 16.7, 14.2, 20.8,
13.4, 11.7, 8.3, 10.2, 10.9, 11. , 9.5, 14.5, 14.1,
16.1, 14.3, 11.7, 13.4, 9.6, 8.7, 8.4, 12.8, 10.5,
17.1, 18.4, 15.4, 10.8, 11.8, 14.9, 12.6, 14.1, 13. ,
13.4, 15.2, 16.1, 17.8, 14.9, 14.1, 12.7, 13.5, 14.9,
20. , 16.4, 17.7, 19.5, 20.2, 21.4, 19.9, 19. , 19.1,
19.1, 20.1, 19.9, 19.6, 23.2, 29.8, 13.8, 13.3, 16.7,
12. , 14.6, 21.4, 23. , 23.7, 25. , 21.8, 20.6, 21.2,
19.1, 20.6, 15.2, 7. , 8.1, 13.6, 20.1, 21.8, 24.5,
23.1, 19.7, 18.3, 21.2, 17.5, 16.8, 22.4, 20.6, 23.9,
22. , 11.9])
datasets.make_regression
<function sklearn.datasets.samples_generator.make_regression>
2. Regression
np.random.seed(123)
X_all, y_all = datasets.make_regression(n_samples=50, n_features=50, n_informative=10)
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X_all, y_all, train_size=0.5)
X_train.shape, y_train.shape
((25, 50), (25,))
X_test.shape, y_test.shape
((25, 50), (25,))
model = linear_model.LinearRegression()
model.fit(X_train, y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
def sse(resid):
return sum(resid**2)
resid_train = y_train - model.predict(X_train)
sse_train = sse(resid_train)
sse_train
1.2995000355014354e-24
resid_test = y_test - model.predict(X_test)
sse_test = sse(resid_test)
sse_test
1.2995000355014354e-24
model.score(X_train, y_train)
1.0
model.score(X_test, y_test)
0.31407400675201746
def plot_residuals_and_coeff(resid_train, resid_test, coeff):
fig, axes = plt.subplots(1, 3, figsize=(12, 3))
axes[0].bar(np.arange(len(resid_train)), resid_train)
axes[0].set_xlabel("sample number")
axes[0].set_ylabel("residual")
axes[0].set_title("training data")
axes[1].bar(np.arange(len(resid_test)), resid_test)
axes[1].set_xlabel("sample number")
axes[1].set_ylabel("residual")
axes[1].set_title("testing data")
axes[2].bar(np.arange(len(coeff)), coeff)
axes[2].set_xlabel("coefficient number")
axes[2].set_ylabel("coefficient")
fig.tight_layout()
return fig, axes
fig, ax = plot_residuals_and_coeff(resid_train, resid_test, model.coef_);
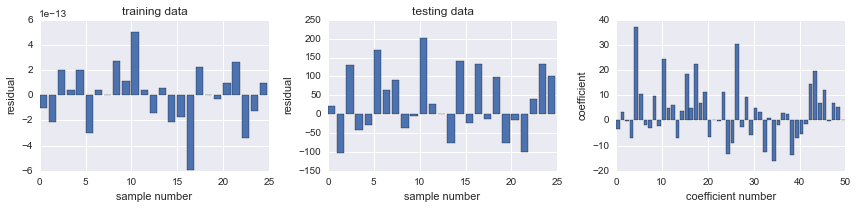
model = linear_model.Ridge(alpha=5)
model.fit(X_train, y_train)
Ridge(alpha=5, copy_X=True, fit_intercept=True, max_iter=None,
normalize=False, random_state=None, solver='auto', tol=0.001)
resid_train = y_train - model.predict(X_train)
sse_train = sum(resid_train**2)
sse_train
3292.9620358692669
resid_test = y_test - model.predict(X_test)
sse_test = sum(resid_test**2)
sse_test
209557.58585055027
model.score(X_train, y_train), model.score(X_test, y_test)
(0.99003021243324718, 0.32691539290134664)
fig, ax = plot_residuals_and_coeff(resid_train, resid_test, model.coef_)
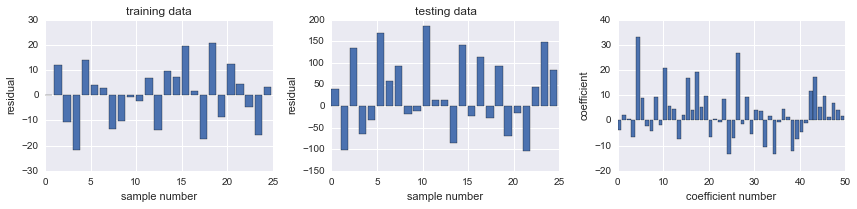
model = linear_model.Lasso(alpha=1.0)
model.fit(X_train, y_train)
Lasso(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=1000,
normalize=False, positive=False, precompute=False, random_state=None,
selection='cyclic', tol=0.0001, warm_start=False)
resid_train = y_train - model.predict(X_train)
sse_train = sse(resid_train)
sse_train
309.74971389532368
resid_test = y_test - model.predict(X_test)
sse_test = sse(resid_test)
sse_test
1489.1176065002649
fig, ax = plot_residuals_and_coeff(resid_train, resid_test, model.coef_)
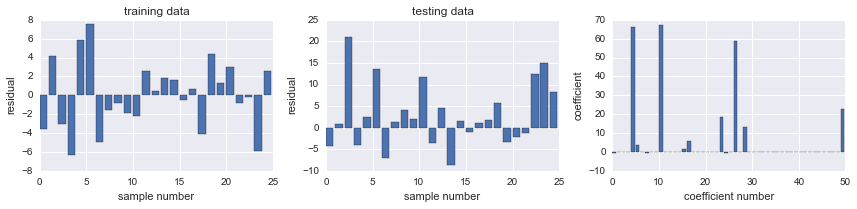
alphas = np.logspace(-4, 2, 100)
coeffs = np.zeros((len(alphas), X_train.shape[1]))
sse_train = np.zeros_like(alphas)
sse_test = np.zeros_like(alphas)
for n, alpha in enumerate(alphas):
model = linear_model.Lasso(alpha=alpha)
model.fit(X_train, y_train)
coeffs[n, :] = model.coef_
resid = y_train - model.predict(X_train)
sse_train[n] = sum(resid**2)
resid = y_test - model.predict(X_test)
sse_test[n] = sum(resid**2)
/Users/xiaokai/anaconda/lib/python2.7/site-packages/sklearn/linear_model/coordinate_descent.py:466: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations
ConvergenceWarning)
fig, axes = plt.subplots(1, 2, figsize=(12, 4), sharex=True)
for n in range(coeffs.shape[1]):
axes[0].plot(np.log10(alphas), coeffs[:, n], color='k', lw=0.5)
axes[1].semilogy(np.log10(alphas), sse_train, label="train")
axes[1].semilogy(np.log10(alphas), sse_test, label="test")
axes[1].legend(loc=0)
axes[0].set_xlabel(r"${\log_{10}}\alpha$", fontsize=18)
axes[0].set_ylabel(r"coefficients", fontsize=18)
axes[1].set_xlabel(r"${\log_{10}}\alpha$", fontsize=18)
axes[1].set_ylabel(r"sse", fontsize=18)
fig.tight_layout()

model = linear_model.LassoCV()
model.fit(X_all, y_all)
LassoCV(alphas=None, copy_X=True, cv=None, eps=0.001, fit_intercept=True,
max_iter=1000, n_alphas=100, n_jobs=1, normalize=False, positive=False,
precompute='auto', random_state=None, selection='cyclic', tol=0.0001,
verbose=False)
model.alpha_
0.06559238747534718
resid_train = y_train - model.predict(X_train)
sse_train = sse(resid_train)
sse_train
1.5450589323148045
resid_test = y_test - model.predict(X_test)
sse_test = sse(resid_test)
sse_test
1.5321417406217364
model.score(X_train, y_train), model.score(X_test, y_test)
(0.99999532217220677, 0.99999507886570982)
fig, ax = plot_residuals_and_coeff(resid_train, resid_test, model.coef_)

3. Classification
iris = datasets.load_iris()
type(iris)
sklearn.datasets.base.Bunch
iris.target_names
array(['setosa', 'versicolor', 'virginica'],
dtype='|S10')
iris.feature_names
['sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)']
iris.data.shape
(150, 4)
iris.target.shape
(150,)
X_train, X_test, y_train, y_test = cross_validation.train_test_split(iris.data, iris.target, train_size=0.7)
classifier = linear_model.LogisticRegression()
classifier.fit(X_train, y_train)
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False)
y_test_pred = classifier.predict(X_test)
print(metrics.classification_report(y_test, y_test_pred))
precision recall f1-score support
0 1.00 1.00 1.00 18
1 1.00 1.00 1.00 14
2 1.00 1.00 1.00 13
avg / total 1.00 1.00 1.00 45
np.bincount(y_test)
array([18, 14, 13])
metrics.confusion_matrix(y_test, y_test_pred)
array([[18, 0, 0],
[ 0, 14, 0],
[ 0, 0, 13]])
classifier = tree.DecisionTreeClassifier()
classifier.fit(X_train, y_train)
y_test_pred = classifier.predict(X_test)
metrics.confusion_matrix(y_test, y_test_pred)
array([[18, 0, 0],
[ 0, 14, 0],
[ 0, 3, 10]])
classifier = neighbors.KNeighborsClassifier()
classifier.fit(X_train, y_train)
y_test_pred = classifier.predict(X_test)
metrics.confusion_matrix(y_test, y_test_pred)
array([[18, 0, 0],
[ 0, 13, 1],
[ 0, 2, 11]])
classifier = svm.SVC()
classifier.fit(X_train, y_train)
y_test_pred = classifier.predict(X_test)
metrics.confusion_matrix(y_test, y_test_pred)
array([[18, 0, 0],
[ 0, 13, 1],
[ 0, 1, 12]])
classifier = ensemble.RandomForestClassifier()
classifier.fit(X_train, y_train)
y_test_pred = classifier.predict(X_test)
metrics.confusion_matrix(y_test, y_test_pred)
array([[18, 0, 0],
[ 0, 14, 0],
[ 0, 2, 11]])
train_size_vec = np.linspace(0.1, 0.9, 30)
classifiers = [tree.DecisionTreeClassifier,
neighbors.KNeighborsClassifier,
svm.SVC,
ensemble.RandomForestClassifier
]
cm_diags = np.zeros((3, len(train_size_vec), len(classifiers)), dtype=float)
for n, train_size in enumerate(train_size_vec):
X_train, X_test, y_train, y_test = \
cross_validation.train_test_split(iris.data, iris.target, train_size=train_size)
for m, Classifier in enumerate(classifiers):
classifier = Classifier()
classifier.fit(X_train, y_train)
y_test_pred = classifier.predict(X_test)
cm_diags[:, n, m] = metrics.confusion_matrix(y_test, y_test_pred).diagonal()
cm_diags[:, n, m] /= np.bincount(y_test)
fig, axes = plt.subplots(1, len(classifiers), figsize=(12, 3))
for m, Classifier in enumerate(classifiers):
axes[m].plot(train_size_vec, cm_diags[2, :, m], label=iris.target_names[2])
axes[m].plot(train_size_vec, cm_diags[1, :, m], label=iris.target_names[1])
axes[m].plot(train_size_vec, cm_diags[0, :, m], label=iris.target_names[0])
axes[m].set_title(type(Classifier()).__name__)
axes[m].set_ylim(0, 1.1)
axes[m].set_xlim(0.1, 0.9)
axes[m].set_ylabel("classification accuracy")
axes[m].set_xlabel("training size ratio")
axes[m].legend(loc=4)
fig.tight_layout()

4. Clustering
X, y = iris.data, iris.target
np.random.seed(123)
n_clusters = 3
c = cluster.KMeans(n_clusters=n_clusters)
c.fit(X)
KMeans(copy_x=True, init='k-means++', max_iter=300, n_clusters=3, n_init=10,
n_jobs=1, precompute_distances='auto', random_state=None, tol=0.0001,
verbose=0)
y_pred = c.predict(X)
y_pred[::8]
array([1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 0, 0, 0, 0, 0, 0], dtype=int32)
y[::8]
array([0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2])
idx_0, idx_1, idx_2 = (np.where(y_pred == n) for n in range(3))
y_pred[idx_0], y_pred[idx_1], y_pred[idx_2] = 2, 0, 1
y_pred[::8]
array([0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2], dtype=int32)
metrics.confusion_matrix(y, y_pred)
array([[50, 0, 0],
[ 0, 48, 2],
[ 0, 14, 36]])





