作业
给定函数f(x) = x^2 + 3*x - 10
- 理解方程求根中的二分法，使用numpy库而非scipy库实现算法
- 使用上述算法求函数f(x)的根
- 理解梯度下降法(gradient descent)，并使用基本的numpy库而非scipy库实现算法
- 使用上述算法来得到函数f(x)的最小值
import numpy as np
import scipy as sp
import scipy.optimize as opt
import matplotlib.pyplot as plt
%matplotlib inline
from sympy import *
x = symbols('x')
fsym = x**2 + 3*x - 10
# 先获取准确值
solve(fsym)
[-5, 2]
plotting.plot(fsym);
二分法
理论依据非常简单，就是若果函数f(x)在区间(a,b)上连续，且f(a)*f(b) < 0，也就是异号，则f(x)=0在区间(a,b)上必有根。进行二分，逐渐缩小区间，直到区间小于设置的误差，取区间均值为根。
二分法是比较简单、但速度较慢的一种求根方法。它的主要思想是：如果 f(a) 和 f(b) 异号，且函数方程连续，那么函数的根一定处在 a 和 b 之间。我们通过中间点 c 来估测方程的根所在的位置。如果 f(c) 为 0， c 即为 函数的根。 如果 f(c) 不为 0， 取 f(a) 和 f(b) 当中与 f(c) 异号的那一个值构建新的求根区间，继续计算中间点求根。
f = lambda x: x**2 + 3*x -10
scipy.optimize.bisect直接求解
f参数: python function returning a number. f must be continuous, and f(a) and f(b) must have opposite signs.
print (opt.bisect(f,-7,0), opt.bisect(f,0,5))
(-4.999999999999659, 1.9999999999998863)
手动实现
def my_bisect(f,a,b,tol=1e-10):
'''
Interval [a, b]
'''
if f(a)*f(b) > 0:
raise ValueError('f(a) and f(b) must have different signs!')
if a > b:
a, b = b, a
c = (a + b)/2.
if f(c) == 0 or (b - a)/2 < tol:
return c
while (b - a)/2. > tol:
if f(a)*f(c) > 0:
a = c
else:
b = c
c = (a + b)/2
return c
结果精度还可以
print (my_bisect(f,-7,0), my_bisect(f,0,5))
(-4.999999999978172, 2.0000000000436557)
牛顿迭代法
这里用牛顿迭代法实现函数求根。牛顿迭代法的基本思想就是用局部的线性近似，用切线代替曲线，其实是泰勒展开，只去线性项:$f(x+h)\approx f(x)+f'(x)h$
如果$x+h$是$f(x)=0$的一个根，即$f(x+h)=0$，则：$h\approx -\frac{f(x)}{f'(x)}$ 以及$x+h\approx x - \frac{f(x)}{f'(x)}$
参考用Python学微积分.
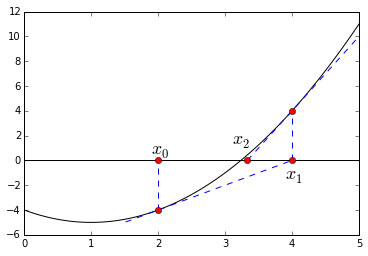可以看到从$x0$到$x_1$到$x_2$的收敛。最后的迭代公式是$x{n+1}=xn-\frac{f(x_n)}{f'(x_n)}$,当$x{n+1}$与$x_n$足够接近的时候，表示结果收敛，可以停止迭代。
def my_newton(f,x0=0,tol=1e-8):
# x0 initial guess
while True:
x1 = x0 - f.subs(x,x0)/f.diff().subs(x,x0)
if np.abs(x1-x0) < tol:
break
x0 = x1
return float(x1)
x = symbols('x')
fsym = x**2 + 3*x - 10
# 需要画图猜出一个靠谱的初始值
for x0 in [-5,2]:
print my_newton(fsym,x0=x0)
-5.0
2.0
可以看出牛顿迭代法，精确度很高的。但是initial guess在-1.5的时候my_newton(f,x0=-1.5)，导数值为0,还是会出现错误,出现分母为0，还需要进一步使方法更健壮，实现的有点简陋。
梯度下降法
梯度下降法是一个最优化算法，通常也称为最速下降法。最速下降法是求解无约束优化问题最简单和最古老的方法之一，虽然现在已经不具有实用性，但是许多有效算法都是以它为基础进行改进和修正而得到的。最速下降法是用负梯度方向为搜索方向的，最速下降法越接近目标值，步长越小，前进越慢。
Wiki上的解释为如果目标函数$F(x)$在点$a$处可微且有定义，那么函数$F(x)$在点$a$沿着梯度相反的方向$-\nabla F(a)$下降最快。其中,$\nabla$为梯度算子，$\nabla = (\frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2}, \ldots, \frac{\partial}{\partial x_n})^T$
什么是梯度下降法？
- 梯度下降法，可作为一种求解最小二乘法的方式，它是最优化中比较古老的一种方法
- 梯度下降，设定起始点负梯度方向 (即数值减小的方向) 为搜索方向，寻找最小值。梯度下降法越接近目标值，步长越小，前进越慢.
# 数学知识可得在对称轴取最小值
a = -1.5
print a**2 + 3*a - 10
-12.25
opt.minimize(f,-1)
fun: -12.25
hess_inv: array([[ 0.50000001]])
jac: array([ 0.])
message: 'Optimization terminated successfully.'
nfev: 12
nit: 2
njev: 4
status: 0
success: True
x: array([-1.50000001])
# 极值点
opt.minimize(f,-1).x
array([-1.50000001])
opt.minimize(f,-1).fun
-12.25
from scipy.optimize import basinhopping
basinhopping(f,x0,stepsize = 5).x
array([-1.49999998])
一维梯度下降算法
# local minimum occurs at x=1.5
# fsym = x**2 + 3*x - 10
def gd(fsym,x0,step=0.01,tol=1e-5):
x1 = x0
while True:
x0 = x1
x1 = x0 - step * fsym.diff().subs(x,x0)
if np.abs(x1-x0) < tol:
break
return x1
print gd(fsym,-1)
-1.49951076900151
二维算例
实现二维梯度下降法的实现，当然可以更也可以写general的方法，思路都是一样的。这里给出一个例子，并首先画图看看函数的性质。
def g(X):
x, y = X
return (x-1)**4 + 5 * (y-1)**2 - 2*x*y
X_opt = opt.minimize(g,(8, 3))
print X_opt
fun: -3.8672228877127943
hess_inv: array([[ 0.11159896, 0.02232105],
[ 0.02232105, 0.10446406]])
jac: array([ -8.94069672e-08, -2.98023224e-08])
message: 'Optimization terminated successfully.'
nfev: 72
nit: 12
njev: 18
status: 0
success: True
x: array([ 1.88292611, 1.37658521])
3D plot
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
fig = plt.figure()
ax = fig.gca(projection='3d')
X = np.linspace(-2,4,100)
Y = np.linspace(-2,4,100)
X, Y = np.meshgrid(X,Y)
Z = g((X,Y))
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
cset = ax.contour(X, Y, Z, zdir='z',offset=-5, cmap=cm.coolwarm)
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()
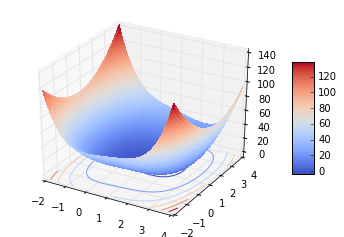
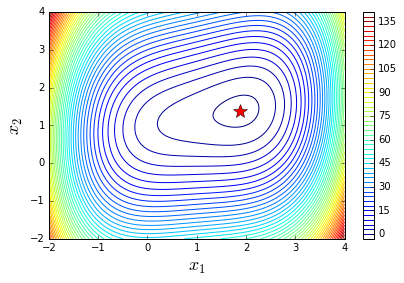
Contour
fig, ax = plt.subplots(figsize=(6, 4))
# get X, Y from above
c = ax.contour(X, Y, g((X, Y)), 50)
ax.plot(X_opt.x[0], X_opt.x[1], 'r*', markersize=15)
ax.set_xlabel(r"$x_1$", fontsize=18)
ax.set_ylabel(r"$x_2$", fontsize=18)
plt.colorbar(c, ax=ax)
fig.tight_layout()
用symbol，方便求导
x, y = symbols('x'), symbols('y')
def gsym(x,y):
return (x-1)**4 + 5 * (y-1)**2 - 2*x*y
# a = gsym().diff
gsym(x,y).diff(x)
-2*y + 4*(x - 1)**3
gsym(x,y).subs({x:1, y:0})
5
二维梯度下降算法
def gd_2d(f,X,step=0.01,tol=1e-3):
X0 = X
def gradient(f,X):
dx = float(f.diff(x).subs({x:X[0], y:X[1]}))
dy = float(f.diff(y).subs({x:X[0], y:X[1]}))
norm = (1./np.sqrt(dx**2+dy**2))
return norm*np.array([dx,dy])
while True:
z0 = float(f.subs({x:X0[0], y:X0[1]}))
X1 = X0 - step*gradient(f,X0)
z1 = float(f.subs({x:X1[0], y:X1[1]}))
if np.abs(z1 - z0) < tol:
break
X0 = X1
return X1
print gd_2d(gsym(x,y),[0,0])
[ 1.88360394 1.37674131]
X_opt.x
array([ 1.88292611, 1.37658521])