衡量中国人的生活水平

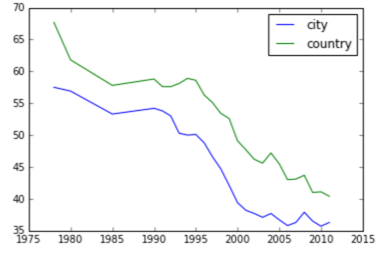
有很多指标可以衡量，比如收入、储蓄、购买食物的支出所占的比例（恩格尔系数），这里仅选取恩格尔系数, 恩格尔系数达59%以上为贫困，50-59%为温饱，40-50%为小康，30-40%为富裕，低于30%为最富裕。当然越低越好了，说明手里有闲钱了。数据来源为国家统计局的城乡居民家庭人均收入及恩格尔系数.变化趋势可以用如下代码生成图形查看。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline 
year = np.array([1978, 1980, 1985, 1990, 1991, 1992, 1993, 1994, 1995, 1996, 1997, 1998, 1999, 2000, 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009, 2010, 2011])
city = np.array([57.5, 56.9, 53.3, 54.2, 53.8,  53.0, 50.3, 50.0, 50.1, 48.8, 46.6, 44.7, 42.1, 39.4, 38.2, 37.7, 37.1, 37.7, 36.7, 35.8, 36.3, 37.9, 36.5, 35.7, 36.3])
country = np.array([67.7, 61.8, 57.8, 58.8, 57.6, 57.6, 58.1, 58.9, 58.6, 56.3, 55.1, 53.4, 52.6, 49.1, 47.7, 46.2, 45.6, 47.2, 45.5, 43.0, 43.1, 43.7, 41.0, 41.1, 40.4])
city_plot, = plt.plot(year, city, label = "city")
country_plot, = plt.plot(year,country, label = "country")
plt.legend(handles=[city_plot, country_plot])

之前是手动复制粘贴的，经竹子提醒，改用非手动的方式，再次尝试用python获取数据，下面是相应的代码。

import requests
from bs4 import BeautifulSoup
import numpy as np
import matplotlib.pyplot as plt

# get data
a = requests.get('http://www.stats.gov.cn/tjsj/ndsj/2012/html/J1002c.htm')
soup = BeautifulSoup(a.text, 'html.parser')
x = soup.find_all(class_='xl29') # year data with class 'xl29'
year = []
for data in x:
    try:
        year.append(int(data.text))
    except:
        continue #skip rows without data

t_data = soup.find_all(class_='xl32') # table data with class 'xl32'
city, country = [],[]
t_data = [x for x in t_data if x.text != ''] #remove empty table data
for i in range(0,len(t_data),5):
    city.append(float(t_data[i+3].text))
    country.append(float(t_data[i+4].text))

# plot
%matplotlib inline
city_plot, = plt.plot(year, city, label = "city")
country_plot, = plt.plot(year,country, label = "country")
plt.legend(handles=[city_plot, country_plot])

运行程序可以得到如上一样的结果。

双盲实验

双盲（double blind）是指：研究对象和研究者都不了解试验分组情况，而是由研究设计者来安排和控制全部试验。双盲实验是一种更加严格的实验方法，通常适用于以人为研究对象的实验（human subjects），旨在消除可能出现在实验者和参与者意识当中的主观偏差（subjective bias）和个人偏好（personal preferences），避免主、被试双方因为主观期望所引发的额外变量，是一种控制变量的方法。

Ngram

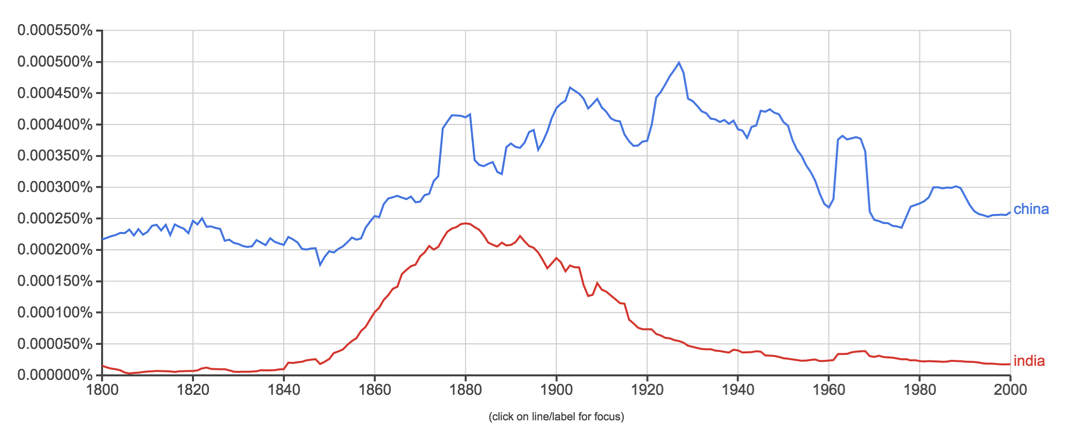
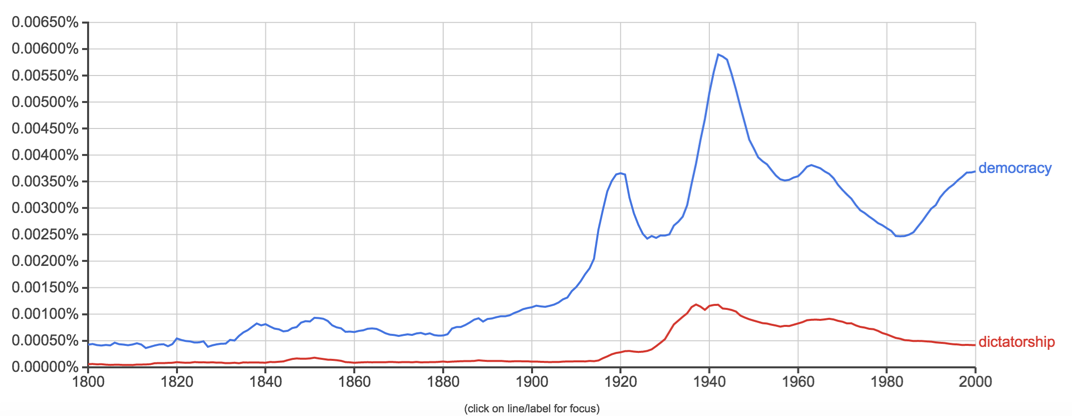
Google实验室推出新产品Books Ngram Viewer，以图示形式显示/对比查询词在1800-2000年间图书中的词频，包括英、法、德、俄、西、汉六种文字。与Google搜索不同的是，查询词是区分大小写的。作为Google图书的一个副产品，在图示下还有查询词在Google图书搜索的链接，且根据词频，分不同的年段。输入你感兴趣的词，瞬间得到词频的变化趋势。

辛普森悖论

辛普森悖论（Simpson's Paradox）亦有人译为辛普森诡论，为英国统计学家E.H.辛普森（E.H.Simpson）于1951年提出的悖论，即在某个条件下的两组数据，分别讨论时都会满足某种性质，可是一旦合并考虑，却可能导致相反的结论。

比如在伯克利录取歧视案例中，从单个学院看，女生的录取比例并不比男生低，甚至还高，但把所以的学院加在一起看，女生的录取率明显下降好多。原因就是默认地给所以的学院分配相同的权重，但各学院学生基数很大，权重的分配还待商榷。所以，为了避免辛普森悖论，需要斟酌各分组的权重，并乘以一定的系数去消除以分组数据基数差异而造成的影响。

贝叶斯定理

练习

已知某种疾病的发病率是0.001，即1000人中会有一个人得病。现有一种试剂可以检验患者是否得病，它的准确率是0.99，即在患者确实得病的情况下，它有99%的可能呈现阳性。它的误报率是5%，即在患者没有得病的情况下，它有5%的可能呈现阳性。现有一个病人的检验结果为阳性，请问他确实得病的可能性有多大？

一个小例子帮助理解

理解贝叶斯的关键是要明白其用新的事件、信息更新原有概率这一过程。就这个例子而言，如果取出一颗糖，不知道什么糖，这时来自哪个碗有一个概率分布，各1/2，但当知道是水果糖这一事实的时候，我们之前的概率分布就可以依据这一信息更新。

练习